確率変数間の関連性をモデル化する方法のコピュラについて紹介します。
あいさつ
こんにちは。AIソリューション開発部の岩田です。業務では広告効果の推定や、広告予算の最適配分を決める手法の開発などを行なっています。今回は、確率変数間の関連性をモデル化する方法のコピュラについて紹介します。このコピュラについては、日本語で読める文献が少ないようなので、本記事が今後利用する方達の参考になれば幸いです。
確率変数間の従属関係
データ分析をしていると、ある変数と別の変数の関連度合い、つまり従属性について定量的に測る場面が多くあります。例えば、気温などの天候情報とある商品の売り上げの関係や賃貸物件の駅からの距離と賃料の関係などが考えられます。一番簡単な方法は、相関係数(ピアソンの積率相関係数)を計算することです。相関係数を計算すれば、二つの確率変数の関連性を定量化でき、区間推定などによってその有意性について議論することができます。しかし、相関係数は対象となる確率変数が多次元正規分布に従っていることを(暗に)仮定しており、その仮定から外れる裾が重い分布を示す変数の場合や正の値をとる変数などの場合には、従属性を十分に捉えることができません。そのような場合でも確率変数同士の従属性を定量化する方法として接合分布関数(コピュラ)があります。
コピュラ
コピュラとは
話を簡単にするために二次元の連続な確率変数の場合について取り扱います。ある確率変数を$X, Y$とします。この二つの変数の確率的な情報は同時分布$P(X, Y)$または分布関数$F(X, Y)$で全て表すことができます。二つの確率変数それぞれの挙動は、分布関数$F_X(X), F_Y(Y)$を用いれば表すことができます。よって、同時分布関数$F(X, Y)$の内、$F_X(X), F_Y(Y)$以外の情報の部分に変数$X, Y$の従属性に関する情報が含まれていることになります。ここで同時分布関数について以下のように式変形を考えます。
同時分布関数の情報は、二つの周辺分布関数$F_X(x), F_Y(y)$と関数$C(u, v), (0 \le u, v \le 1)$に分解できることがわかります。この最後の周辺分布の情報を含まない変数同士の従属性を表す関数$C(u, v)$をコピュラと呼びます。実務的には、従属性のある多変量なデータを分析するときは、それぞれが正規分布になるように変数変換して多変量正規分布を用いてモデル化することがありますが、変数変換をするのが難しい場合などの多変量正規分布を用いた分析だけでは難しいことがあります。そのような場合、各変数を周辺分布$F_X(X), F_Y(Y)$を用いて表現し、従属性の部分をコピュラ$C(u, v)$を使ってモデル化するというような柔軟な分析も可能となります。
アルキメデス型のコピュラ
それでは、従属性を表す関数$C(u, v)$は、実際にどのような形になるのでしょうか。二変量正規分布に従う確率変数$X, Y$が従うコピュラは正規コピュラまたはガウスコピュラと言い以下のように表されます。
ここで$\Phi_{\rho}(x, y)$は相関係数$\rho$の二次元標準正規分布の同時分布関数、$\Phi(x)$は標準正規分布の分布関数を表します。つまり、多変量正規分布に従う変数のコピュラは初等関数を用いて記述することができません。ここで、以下のように関数$\phi(x):[0,1] \rightarrow [0,\infty], \phi(1)=0$を用いて
によって定義されるコピュラを$\phi(x)$を生成作用素とするアルキメデス型コピュラといいます。 分析でコピュラを使用するのに、コピュラが初等関数を用いて記述できる方が便利です。関数$\phi(x)$を変えることによって、以下のように初等関数で記述できるコピュラを作ることができます。
- クレイトンコピュラ:
- フランクコピュラ:
- グンベルコピュラ:
従属性を表す指標との関係
コピュラには、確率変数同士の従属性の情報が全て含まれています。一方で、その従属性の一面でも捉えることができる簡易な指標の方が実用上は便利です。ピアソンの積率相関係数は確率変数同士の関係を表す指標ですが、冒頭で紹介したように、周辺分布の形によって影響を受けてしまいます。代わりの指標として、ケンドールの順位相関係数やスピアマンの順位相関係数があります。例えば、ケンドールの順位相関係数$\rho_\tau[X,Y]$は
と計算されます。ここで$(X^\prime, Y^\prime)$は$(X,Y)$とは独立に$(X,Y)$と同一の分布に従う確率変数です。式から明らかなように、確率変数の大小に注目していて周辺分布の形によらずに確率変数同士の従属性を表していることがわかります。コピュラは、従属性に関する情報を全て持っているのでした。実は、アルキメデス型のコピュラを持つ確率変数$X, Y$に対するケンドールの順位相関係数は
と計算することができます。
コピュラの推定
ここまで確率変数同士の従属関係を捉えるコピュラについて説明しました。以下では、実際の活用例を紹介します。コピュラの推定にはstatsmodelsを使用します。分析するデータは、政府統計の総合窓口(e-Stat)で公開されている学校保健統計調査の身長と体重の相関表及び身長別体重の平均値のデータ(17歳男性)を参考にして作成したデータです。データをプロットしてみると、身長は正規分布のような形を示しますが、体重の分布が上側に裾の重い分布を示していることがわかります。さらに散布図から、体重の上側の裾の部分は身長の高い人たちに多く見られる傾向がわかります。
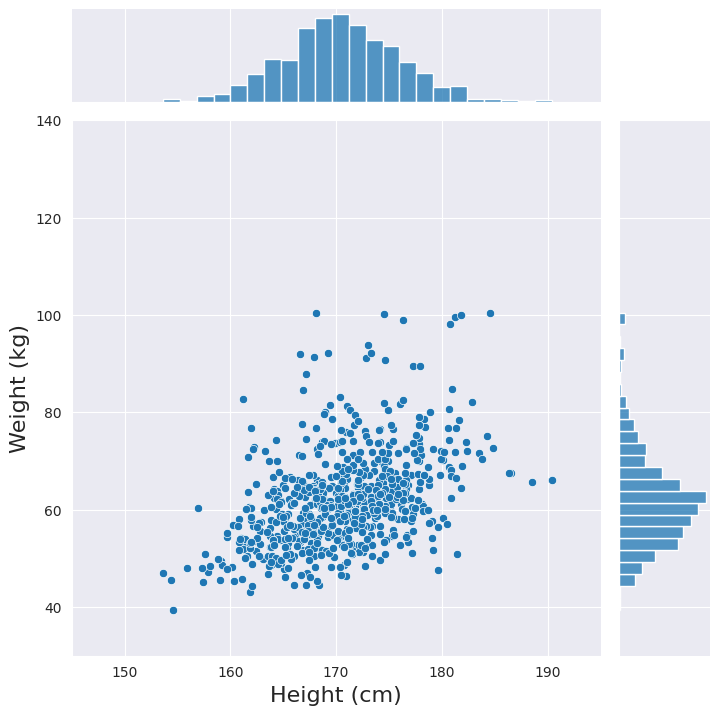
今回は、身長と体重の周辺分布をそれぞれ正規分布とJohnsonSU分布としました。身長のデータに正規分布を当てはめるとパラメータは$(loc, scale)=(170.55, 5.58)$、体重のデータにJohnsonSU分布を当てはめるとパラメータは$(a, b, loc, scale)=(-2.00, 2.35, 46.73, 14.44)$となりました。コピュラの推定にはグンベルコピュラを用い、推定の結果パラメータ$\theta=1.46$でした。推定したコピュラ$C(u, v)$を可視化すると以下のようになります。
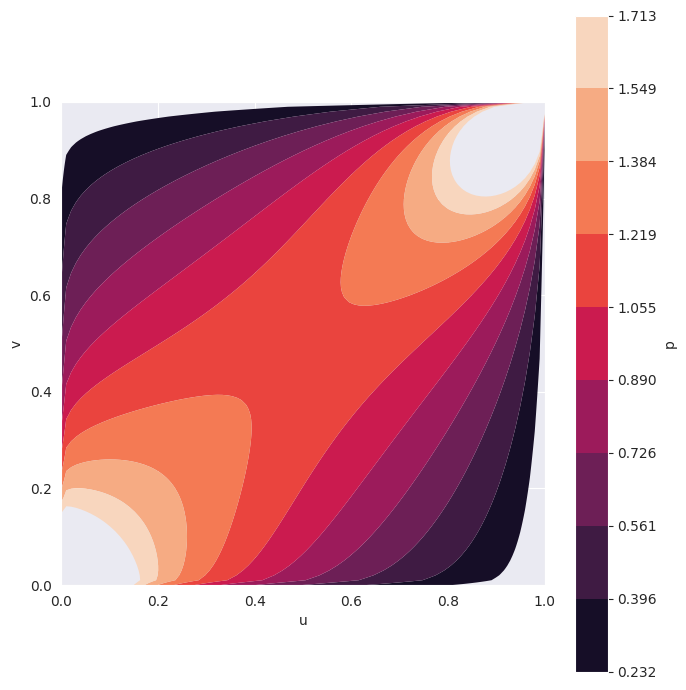
推定した周辺分布とコピュラを使って、身長と体重の同時分布のデータをシミュレートすると以下の散布図のようになります。
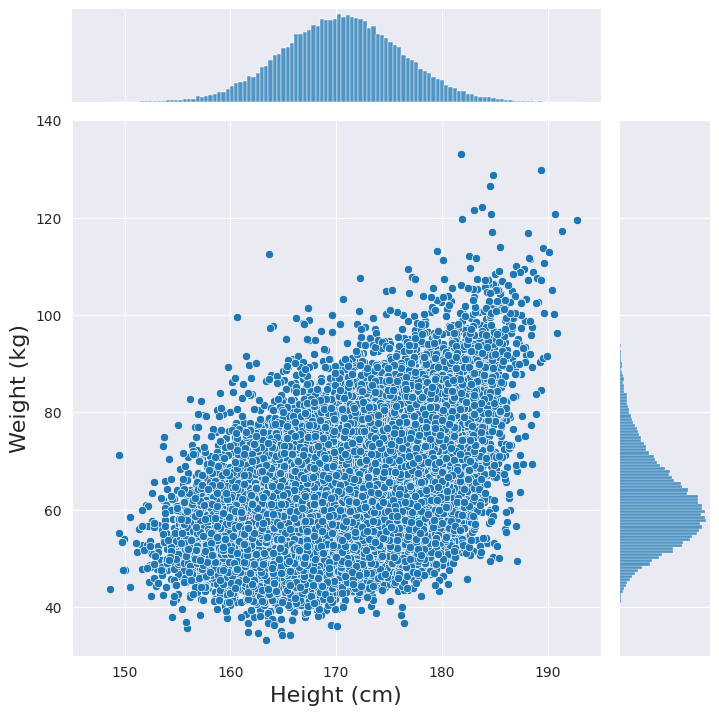
単純に多変量正規分布を当てはめる推定では捉えにくいような身長と体重の非対称な関係性がわかります。このように身長と体重の従属関係を推定してデータを生成することができれば、例えばBMIのような各変数から計算される数値の分布がどのようになっているのかを知ることができます。
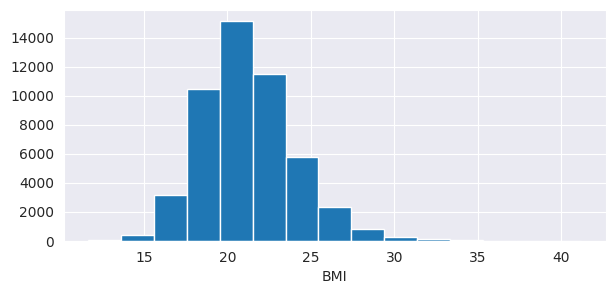
まとめ
確率変数の従属性を推定するコピュラの概要と活用例を紹介しました。金融などのリスクの従属性の評価などに応用されることが多いのですが、それにとどまらず幅広く活用できるのではないかと思います。比較的、文献などが少ない話題なので、この記事が何かの役に立てば良いなと思います。
参考文献・出典
- 岩沢宏和・黒田耕嗣,2015,損害保険数理,日本評論社
- 岩沢宏和,リスクを知るための確率・統計入門,東京図書
- 政府統計の総合窓口(e-Stat)(https://www.e-stat.go.jp/)
Opt Technologies ではエンジニアを募集中です。カジュアル面談も可能ですので、下記リンク先よりお気軽にご応募ください。
